Friday, January 22, 2010

The Big Bang Equations

We can also derive some basic facts about the big bang cosmology. Let us assume the universe is not only expanding but also homogeneous and isotropic. The expansion of the universe is vouched for by the redshifts of distant galaxies. The other assumptions also seem to be approximately correct, at least when we average over small-scale inhomogeneities such as stars and galaxies. For simplicity, we will imagine the universe is homogeneous and isotropic even on small scales.

An observer at any point in such a universe would see all objects receding from her. Suppose that, at some time $t=0$, she identifies a small ball $B$ of test particles centered on her. Suppose this ball expands with the universe, remaining spherical as time passes because the universe is isotropic. Let $R(t)$ stand for the radius of this ball as a function of time. The Einstein equation will give us an equation of motion for $R(t)$. In other words, it will say how the expansion rate of the universe changes with time.

It is tempting to apply equation (2) to the ball $B$, but we must take care. This equation applies to a ball of particles that are initially at rest relative to one another -- that is, one whose radius is not changing at $t=0$. However, the ball $B$ is expanding at $t=0$. Thus, to apply our formulation of Einstein's equation, we must introduce a second small ball of test particles that are at rest relative to each other at $t=0$.

Let us call this second ball $B'$, and call its radius as a function of time $r(t)$. Since the particles in this ball begin at rest relative to one another, we have

\begin{displaymath}\dot r(0) = 0. \end{displaymath}

To keep things simple, let us also assume that at $t=0$ both balls have the exact same size:
\begin{displaymath}r(0) = R(0) .\end{displaymath}

Equation (2) applies to the ball $B'$, since the particles in this ball are initially at rest relative to each other. Since the volume of this ball is proportional to $r^3$, and since $\dot r = 0$ at $t=0$, the left-hand side of equation (2) is simply

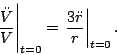
\begin{displaymath} \left.{\ddot V\over V}\right\vert _{t=0}=\left.{3\ddot r\over r}\right\vert _{t=0}. \end{displaymath}

Since we are assuming the universe is isotropic, we know that the various components of pressure are equal: $P_x = P_y = P_z = P$. Einstein's equation (2) thus says that
\begin{displaymath}\left.{3\ddot r\over r}\right\vert _{t=0} = -{1\over 2}(\rho + 3 P) .\end{displaymath}

We would much prefer to rewrite this expression in terms of $R$ rather than $r$. Fortunately, we can do this. At $t=0$, the two spheres have the same radius: $r(0)=R(0)$. Furthermore, the second derivatives are the same: $\ddot r(0) = \ddot R(0)$. This follows from the equivalence principle, which says that, at any given location, particles in free fall do not accelerate with respect to each other. At the moment $t=0$, each test particle on the surface of the ball $B$ is right next to a corresponding test particle in $B'$. Since they are not accelerating with respect to each other, the observer at the origin must see both particles accelerating in the same way, so $\ddot r(0) = \ddot R(0)$. It follows that we can replace $r$ with $R$ in the above equation, obtaining

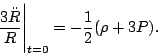
\begin{displaymath}\left.{3\ddot R\over R}\right\vert _{t=0} = -{1\over 2}(\rho + 3 P) .\end{displaymath}

We derived this equation for a very small ball, but in fact it applies to a ball of any size. This is because, in a homogeneous expanding universe, the balls of all radii must be expanding at the same fractional rate. In other words, $\ddot R/R$ is independent of the radius $R$, although it can depend on time. Also, there is nothing special in this equation about the moment $t=0$, so the equation must apply at all times. In summary, therefore, the basic equation describing the big bang cosmology is

\begin{displaymath}{3\ddot R\over R} = -{1\over 2}(\rho + 3 P), \end{displaymath} (3)

where the density $\rho$ and pressure $P$ can depend on time but not on position. Here we can imagine $R$ to be the separation between any two `galaxies'.

To go further, we must make more assumptions about the nature of the matter filling the universe. One simple model is a universe filled with pressureless matter. Until recently, this was thought to be an accurate model of our universe. Setting $P=0$, we obtain

\begin{displaymath}{3\ddot R\over R} = -{\rho \over 2} . \end{displaymath}

If the energy density of the universe is mainly due to the mass in galaxies, `conservation of galaxies' implies that $\rho R^3 = k$ for some constant $k$. This gives
\begin{displaymath}{3\ddot R\over R} = - {k \over 2 R^3} \end{displaymath}

or
\begin{displaymath}\ddot R = -{k \over 6 R^2} .\end{displaymath}

Amusingly, this is the same as the equation of motion for a particle in an attractive $1/R^2$ force field. In other words, the equation governing this simplified cosmology is the same as the Newtonian equation for what happens when you throw a ball vertically upwards from the earth! This is a nice example of the unity of physics. Since ``whatever goes up must come down -- unless it exceeds escape velocity,'' the solutions of this equation look roughly like this:

[01]

So, the universe started out with a big bang! It will expand forever if its current rate of expansion is sufficiently high compared to its current density, but it will recollapse in a `big crunch' otherwise.


Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)